Regla De Tres Compuesta
Regla de tres compuestas (de dos o más reglas simples encadenados)
Se emplean cuando se relacionan más magnitudes de modo a que a partir de las relaciones establecidas entre las magnitudes conocidos se obtenga la magnitud desconocida.
una regla de tres compuesta se compone de varias reglas de tres simples aplicados sucesivamente, es decir que es una cadena continua de reglas de tres simples.
SE DISTINGUEN TRES CASOS:
✔ Regla de tres compuesta DIRECTA
✔ Regla de tres compuesta INVERSA
✔ Regla de tres compuesta MIXTA
la diferencia es la relación entre las magnitudes conocidas y desconocidas
Regla de tres compuesta; Procedimiento General
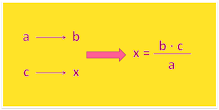
🆇 Relación entre magnitudes: Cada magnitud se analiza con la magnitud desconocido para encontrar su proporcionalidad.
🆈 Se colocan en una tabla; Las magnitudes se colocan en una tabla de acuerdo con su relacion con la magnitud desconocida.
🆉 Se realizan las operaciones; se realizan las simplificaciones para encontrar el valor de la magnitud desconocida.
✔ EJEMPLO GENERAL
Con 8 chorros prendidos por 10h, al día se pagó un consumo de 400Q. se quiere saber cuánto se debe de pagar si se utilizan 16 chorros durante 12h al día en los mismos días.
(Se construye una tabla en la que se comparen las magnitudes previas con las nuevas para determinar el valor de la magnitud desconocido)
Tabla de magnitudes
MAGNITUDES:
CONDICIONES PREVIAS:
CONDICIONES NUEVAS:
Directa o inversa: se analiza si la proporcionalidad de cada magnitud con la magnitud desconocida
pesan 2 botellas de 3lt cada una?
❌ En 4 días, 6 impresoras han impreso 100 libros. ¿Cuántos días tardaran en imprimir 50 libros si tenemos 4 impresoras?
Las magnitudes que tenemos en el problema son; Días, impresoras y libros. La relación entre ellas es.
Analizamos las proporcionalidades entre las magnitudes.

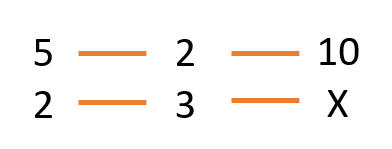

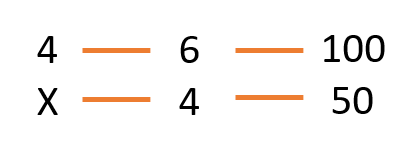

Comentarios
Publicar un comentario